Young A. Consistency Without Inference: Instrumental Variables in Practical Application[R].Working Paper,2017.

摘要：本文采用自助法，对美国经济学会（AEA）顶级期刊上发表的32篇论文中采用的1400个工具变量回归进行了全面的抽样调查，结果表明：工具变量估计经常被发现是虚假显著的，且较OLS对异常值更敏感，同时在总体矩附近有更高的均方差。很少有证据表明OLS估计是实质上的有偏的，反而工具变量经常是不恰当的。另外，本文还发现，建立在弱工具变量基础上的前期检验在很大程度上并不具有参考价值，弱工具变量稳健性分析方法通常不会比2SLS表现更好。

一、引言

经济学界正处于“可信性革命”（Angrist and Pischke,2010）中，其中精心的研究设计已经成为应用研究的必要特征。这场革命的一个关键元素是使用工具变量消除因普通最小二乘法回归造成的内生潜在偏误，从而确定因果效应。然而，研究者在对推理质量越来越重视的同时，对研究设计的重视仍然不足。

尽管Eicker（1963）、Hinkley（1977）、White（1980）的稳健性和聚类协方差估计值被广泛使用，无限样本异方差和相关误差仍然会产生检验统计量其分布通常比想象中分散得多。

这使得普通和两阶段最小二乘法的推理复杂化，尤其是后者更趋于复杂化，其第一阶段联合检验统计量被用来支持第二阶段结果的可信度。本文展示了两阶段最小二乘法（以下简称2SLS或IV），它产生的估计在实际很少比普通最小二乘法（OLS）能更精确地或实质上区别地识别感兴趣的参数。

本文使用自助法来研究美国经济学会（AEA）顶级期刊上发表的32篇论文中的1400次2SLS回归的1533工具变量系数的综合样本的检验统计分布。在整个过程中，本文始终坚持这些作者使用的确切规范及其排除变量与第二阶段残差正交的识别假设。本文在使用自助法时，以与实验组内的误差依赖性和作者标准误差计算所指实验组间的独立性相一致的方式绘制样本。

因此，本文并不关注点估计或基本假设的有效性，而是关注作者在其所建立框架内推理的质量。此外，自举法还表明，传统检验的拒绝率远高于名义规模，即系统地低估置信区间，并且这些失真在联合检验中扩大了。

二、方法

遵循标准的表示法，用小写粗体字母表示矢量和大写粗体字母矩阵，数据生成过程如下给出：

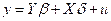(1)

(2)

其中y是第二阶段结果的n×1向量，Y是内生回归因子的n×k_Y矩阵，X是包含的外生回归因子的n×k_X矩阵，Z是排除的外生回归因子（工具）的n×k_Z矩阵，u是n1向量第二阶段干扰，以及第一阶段干扰的n×k_Y矩阵。其余（希腊语）字母是参数，β代表感兴趣的参数。干扰变量X及其相关参数没有实质意义，因而本文用〜来表示X上投影的残差，并用这些残差表征所有的残差。例如，用^表示估计值和预测值，OLS和2SLS的系数估计值由下式给出：

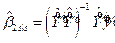,,其中(3)

（b）自举

传统的计量经济学使用假设和渐近定理推断从F₀无限分布母体中提取的具有F1经验分布的样本的f统计量分布，将其被描述为f（F₁ | F₀），并利用自举法估计并观察通过从总体样本F₁中提取的随机样本F₂的分布f（F₂| F₁）(Hall 1992)。如果f是样本的平滑函数，那么自举分布将逐渐收敛到真实分布（Lehmann and Romano,2005），而从无限样本F₁抽取样本F₂时，观察到的结果接近从实际总体样本F₀中抽取的样本F₁。

利用两个自举来测试统计信息。第一个是bootstrap-c，使用自举系数分布来计算协方差矩阵和Wald统计量，概率表示如下：

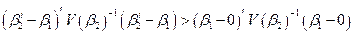(4)

其中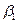是样本F₁估计系数的向量，是F₂样本第i次抽取的估计系数向量，是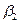的协方差矩阵，0是在总体样本的零假设。在单个系数的情况下，可以消除两边分母的公共方差，减少计算概率：

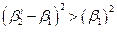(5)

如果系数的分布是无偏的，那么这相当于计算其方差，然而任何方差估计值都会受到抽样变化的影响。由于用于评估检验统计量的分布在临界值附近为凸函数，这种变化趋于产生更大值。如前所述，通过引导自举进行迭代，相当于估计方差的方差，该方差可用于调整临界值。进一步的迭代反过来可以估计这个估计的方差，在每个阶段，人们可以进一步推测Mosteller and Tukey（1977）所谓的统计推理的“迷雾阶梯”，得出先前估计方差的方差估计值。

本文使用的第二种自举措施是bootstrap-t，它使用迭代协方差估计来计算Wald统计量，计算概率：

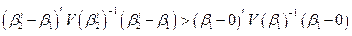(6)

其中是第i个抽样中计算的的常规协方差估计，是初始样本的常规协方差估计。在单个系数的情况下，这相当于估计t统计量平方概率的分布：

(7)

其中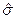表示系数的估计标准误差。如果系数和标准误差满足正态分布，则这相当于计算t分布的自由度，以确定方差的方差。因此，原则上bootstrap-t可以将放置在“迷雾阶梯”之上，达到更高的精确度，而不需要迭代自举的计算成本。然而这依赖于传统的方差估计的精确性。如果常规方差估计值较差，那么bootstrap-t可能会比bootstrap-c更准确，因为它只是将噪声添加到估计的系数分布中（比较方程（4）和（6）），不提供系数方差的方差的期望估计，而只是方差的噪声估计。

本文发现，在2SLS估计的情况下，如果传统的方差估计非常不准确，那么bootstrap-t的准确度就不如bootstrap-t-c，而在OLS估计的情况下，常规方差估计更接近实际系数，其表现也很好，并且通常比bootstrap-c好得多。

三、无推理的一致性

表1报告了使用常规和自举法的变量系数的统计显著性。表的第一行给出了使用作者的协方差计算方法和所选择（正态或t）分布的回归情况，两阶段最小拒绝率系数在1%显著水平下为0.322，在5%显著水平下为0.502。由于作者使用不同的方法，表的其余部分，以及下面的进一步分析，使用一致的格式和分布评估结果。表的第二行给出了使用稳健性协方差矩阵或聚类协方差矩阵对每个方程回归的情况，表的第三行使用默认的协方差估计，两者均使用具有相同自由度和有限样本协方差调整的t分布作为OLS进行评估，以便于与该方法进行比较。正如预期的那样，相对于那些第一行中由作者的回归（多半使用正态分布），使用t分布略微降低显著性，同样如预期的那样，默认的协方差估计会产生较高的拒绝率。

使用不同的常规分布或协方差估计所产生的变化相对于运用自举法的发现是微不足道的。如表1所示，当使用t统计量分布（bootstrap-t）来评估显着性时，显着性水平在每个水平下降约为1/3，而当使用系数分布（bootstrap-c）时，显着性水平下降1/2，p值有实质性的变化。使用作者方法的在1%水平下显著的2SLS系数中，平均p值从0.4%上升到4%，其中1/4显示自举法p值超过5.2%，而具有逆转的意义的是，bootstrap-c的p值平均值从0.3%上升到7.5%，其中1/4自举法p值超过10.8%。

本文样本中所有32篇论文中使用作者方法的，至少有1篇变量系数至少在5%水平下显著，除了4篇之外，所有的论文的变量系数至少在1%水平下显著。分别使用自举法bootstrap-t和bootstrap-c，各有3篇和6篇论文没有5%水平下显著的系数，各有1篇和14篇论文，在任何情况下没有1%水平下显著的系数。

表1 系数意义：使用常规方法和自举法的拒绝率和大小失真

四、结论

当代工具变量实践涉及第一阶段F统计量的基础上报告结果的筛选，因为除了支持工具变量的超前性的论证之外，结论是否接受依赖于第一阶段强关系的证据。本文的结果表明，这种方法非但没有帮助，而且可能有害。传统的Fs没有基于渐近IID的临界值提出大小和偏误的界限。在弱条件下，Fs小于1时，传统的第一阶段F统计量与大小无关，与偏误或均方误差无统计学上的显著关系。相反，当被排除的工具与内生的第二阶段变量之间完全不相关时，出现大F的可能性很大，在这种情况下，在样本中第一阶段F的聚类/稳健标准误或默认协方差的概率大于10%，分别超过8%和20%。在一个经济学家在他们的办公室实验中使用合理工具的世界里，公开报告的结果可以很容易地通过一些工具来填补，尽管这些工具在人口中是外生的，但仍然不相关或非常接近，而强烈报告的是，F很不幸是一个与内生扰动相关有限样本的结果，产生了令人不愉快的偏误估计。当前日益广泛使用检验统计量来获得基于非信息临界值的可信度，其结果并不理想。

经济学家使用2SLS方法，因为他们希望获得感兴趣的更准确的参数估计，在这方面，明确考虑2SLS和OLS之间的权衡似乎很自然。在建立现代2SLS的概念基础时，Sargan（1958）认为，鉴于它们的低效率，只有当它们的置信区间不包括OLS点估计值时才考虑2SLS结果。早些时候，基于OLS无偏时2SLS的低效率以及工具变量不相关时有限样本“识别”的危险，我建议将自举Durbin-Wu-Hausman和工具变量相关性测试作为最小预测试，然后考虑Sargan准则，但是这些方法也会丢掉信息。Feldstein（1974）提出了一种更系统化的替代方案，即使用均方误差估计值来形成2SLS和OLS估计量的加权平均值。

自举法通过估计给定论文样本的时刻下的相对偏误和均方误差，可用来对更广泛的样本作出推论，该方法值得进一步探索。(胡春阳 周玉龙)

 资料来源：http://202.113.18.146/cache/2/03/personal.lse.ac.uk/37bc09f1e99f4d4fdf40762b07926d1b/ConsistencyWithoutInference.pdf