文献来源:Elias Oikarinen, Steven C. Bourassa, Martin Hoesli, Janne Engblom,U.S. metropolitan house price dy namics [J]. Journal of Urban Economics, 2018, 105: 54-69.
摘要:根据美国70个大都市数据,本文探索了房价动态的空间异质性。本文使用了允许空间异质性、横截面以来以及非平稳数据的空间计量先进方法,检验了住宅供给弹性、价格收入弹性以及泡沫的大小和存续期的空间差距和关系。结果表明,房价相对于个人总收入长期弹性平均为0.81,但会随都市区域而发生改变。长期收入弹性一般在供给弹性不足的都市更大,泡沫的大小和存续期和供给弹性的关系则相反。短期增长趋势和调整速度也表现显著的空间异质性。
一、引言
城市经济学理论和实证研究都表明了房价动态空间异质性的存在,依旧假设同质性,会带来预测的误差、政策工具使用的次优等问题。目前,一些学者已在房价动态异质性问题做出了一些贡献,但相关的研究仍然较少。本文致力于分析动态的空间差异,通过美国70个大都市1980Q1-2015Q2的季度数据,探究了长期收入弹性和短期动态的城市级差距。本文的分析是对传统空间同质性假设的检验。
二、理论框架
本文实证研究的基础模型采用了传统的住宅市场存量-流量模型,具体形式如下:
其中,dit、sit分别表示城市i第t期的住宅需求和供给;y为总收入,表示城市购买力;r为利率,表示资本的机会成本;p为房价,c为住宅修建成本;除利率外,数据均采用log形式。参数γ1表示相对于总收入的需求弹性;γ2表示利率对需求的影响;γ3、φ1表示需求和供给的价格弹性;φ2表示相对于修建成本的长期供给弹性。
实际生活中,由于信息不对称以及市场摩擦,价格总是偏离均衡。结合空间异质性的存在,定义价均衡价格方程和价格调整方程如下:
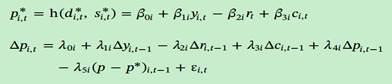
三、实证分析
第一阶段,首先使用CIPS面板单位根检验了数据的平稳性问题。结果表明价格、总收入、修建成本显著为非平稳,其差分形式(即增长率)是平稳的。这表明第二阶段有必要进行协整检验,并采取适用非平稳数据的估计方法。
第二阶段,估计了长期房价方程。本文首次尝试运用FMOLS-AMG方法分析房价动态(完全修正的增广组均值OLS估计),该方法相对于传统的组均值估计方法有很多优势,除此外,还使用了MG(组均值估计)、FMOLS-MG(完全修正的组均值估计)、CCEMG(共同相关效应组均值估计)、DCCEMG(动态CCEMG)作为对照。结果表明,收入价格弹性表现出空间异质性,底特律最高,沃斯堡最低,海岸、湖滨城市一般弹性较高,组均值系数估计(β1)显著为0.81。由于受到管制等因素的影响,收入弹性与供给弹性呈反向关系,即供给弹性越小,收入弹性越大。
第三阶段,估计价格调整方程,聚焦短期房价动态。本文使用了DCCEMG估计了增长趋势以及向长期均调整的速度,使用OLS、RE、MG、CCEMG作为对照。结果发现,短期增长趋势系数(λ1)显著为0.17,价格调整速度(λ5)显著为4.6%。
最后,进行了围绕长期基本价格的房价波动研究。本文将70市分为11个区域,结果表明房价围绕长期均衡波动,同区域内房价变化趋势基本一致。这些偏离均衡的波动也可以研究房地产泡沫问题,长期泡沫存在于供给缺乏弹性的城市。
四、结论
传统面板模型存在很多问题,尤其是在空间领域。考虑异质性的模型能产生更准确的估计结果,对于房价均衡水平、泡沫的测算、房地产政策、都市增长期望以及当地房地产都有很好的经济指导含义。此外,本文的研究还考虑了横截面依赖性,不考虑这些因素会使得增长势头的估计结果过高,价格调整速度估计过低甚至相反的参数估计符号。虽然本文分析了房价动态和供给弹性的关系,但未来应该进一步研究需求弹性和房价动态的关系。(张伟静,周玉龙)
